Modelling and inference for spatiotemporal geodetic data with applications to terrestrial radar interferometry

Data gathered by terrestrial radar interferometry (TRI) exhibits complicated artifacts with nontrivial spatiotemporal correlation structure that can mask any measured deformations entirely. Stochastic estimation tasks posed for data stemming from measurements made by TRI are complicated furthermore by the fact, that stochastic models describing reliably the correlation structure encountered in TRI-data are not yet commonly available and need to be learned from observations.

Rendered image of a radar acquisition in a mountain range. — Fig. 1: Model of the measurement process underlying terrestrial radar interferometry. The Measurements assigned to one pixel in an radar image are impacted by the random and systematic effects occurring along the way of propagation.

It is possible to formulate the task of extracting deformations from TRI-data as an optimization problem in reproducing kernel Hilbert space (RKHS) – a space of functions furnished with probability measure in which maximum likelihood estimation corresponds to norm minimization and solutions to both are called splines. The relationship between different types of splines like interpolating and smoothing splines was investigated and their physical interpretation in the context of TRI have been shown. Tensor product decompositions and numerical cubature have been employed to derive computationally feasible implementations to full spatiotemporal estimation problems.

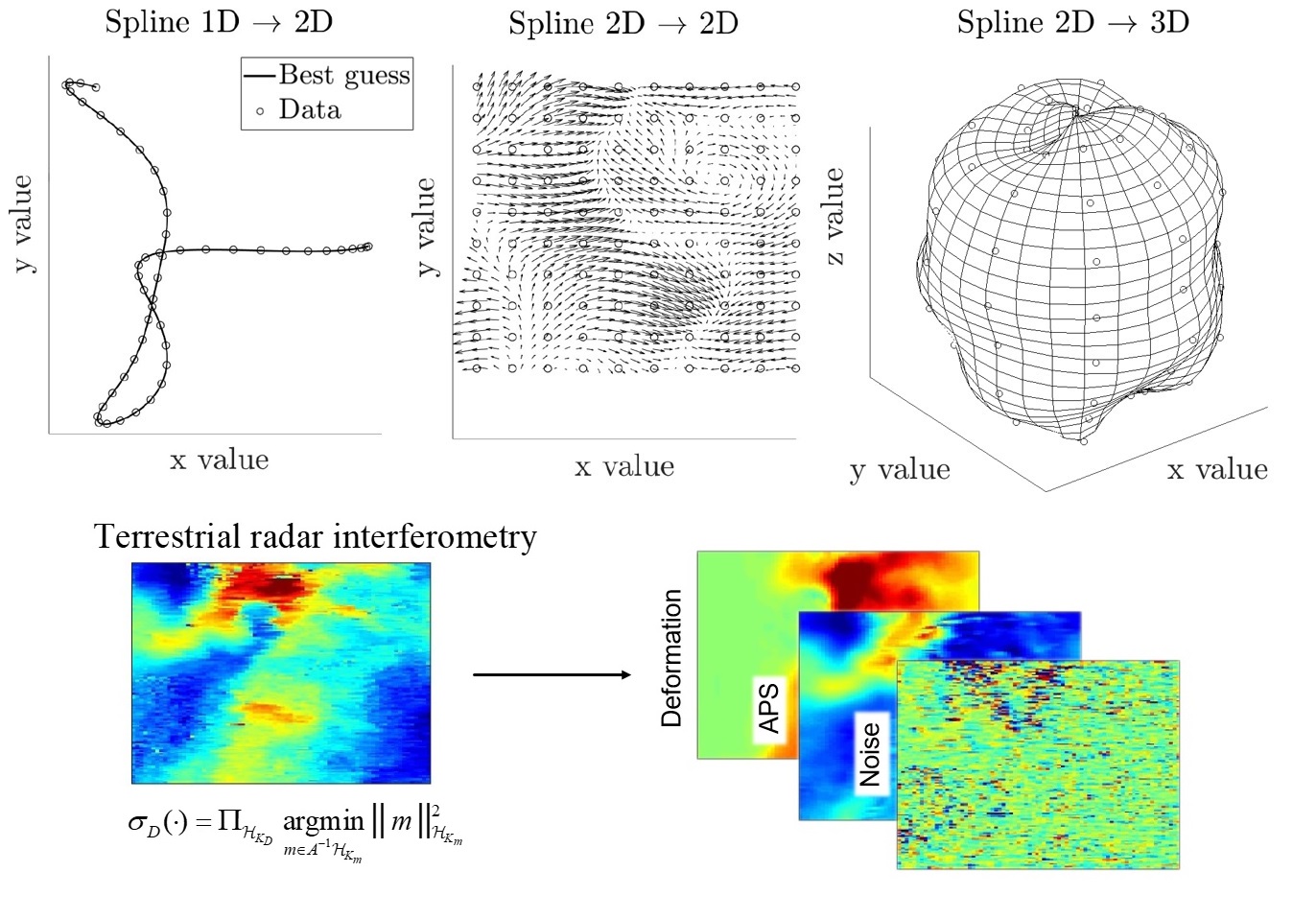
Image of splines in several dimensions and the TRI signal separation problem — Fig. 2: The solutions to minimization problems in RKHS are called splines and solve and solve a diverse set of estimation tasks. Signal separation for TRI is a complicated statistical problem posable as a minimum-norm problem in a RKHS.

The Moore-Aronzsajn theorem shows that both structure and probability measure associated to an RKHS are in one-to-one correspondence to positive definite kernels and consequently the task of learning the probability distribution over Hilbert space most likely given the observations can be reduced to inferring a positive definite kernel. To this effect we are working on establishing a Wishart-type distribution over the coefficient tensors that arise when positive definite kernels are represented as a superposition of tensor products of orthonormal basis functions generalizing the classical Mercer decomposition to enable maximum aposteriori estimation of kernels. A scheme for gradient descent through the convex cone of all kernels has been tested and delivers promising results; Python-based open source implementations are publicly available.. Apart from this, general interactions between machine learning and geodetical data analysis have been examined including high-level correspondences between concepts in both disciplines and several nontrivial examples made public in the form of papers, tutorials, and sample code. .

Image of a 3-dimensional convex cone with gradient vectors — Fig. 3: An illustration of a convex cone of positive definite matrices. Following the gradient flow yields a kernel representing a mixture knowledge from prior considerations and data.

Contact

Dr. Jemil Avers Butt

Lecturer at the Department of Civil, Environmental and Geomatic Engineering

Geosensorik und Ingenieurgeodäsie
Stefano-Franscini-Platz 5
8093 Zürich
Switzerland