Data Analysis

Real-world geodetic data gathered with modern instruments are often spatiotemporal in nature and exhibit complicated deterministic and stochastic behavior due to the presence of measurement uncertainty and the physical complexities inherent the measurement process. For measurement systems acting via electromagnetic waves and including the optical range, electronic crosstalk, the influence of meteorological effects and the properties of the surveyed objects themselves can have a significant impact on the data. This results in datasets with highly intricate correlations that are hard to capture in terms of simple parametric models.

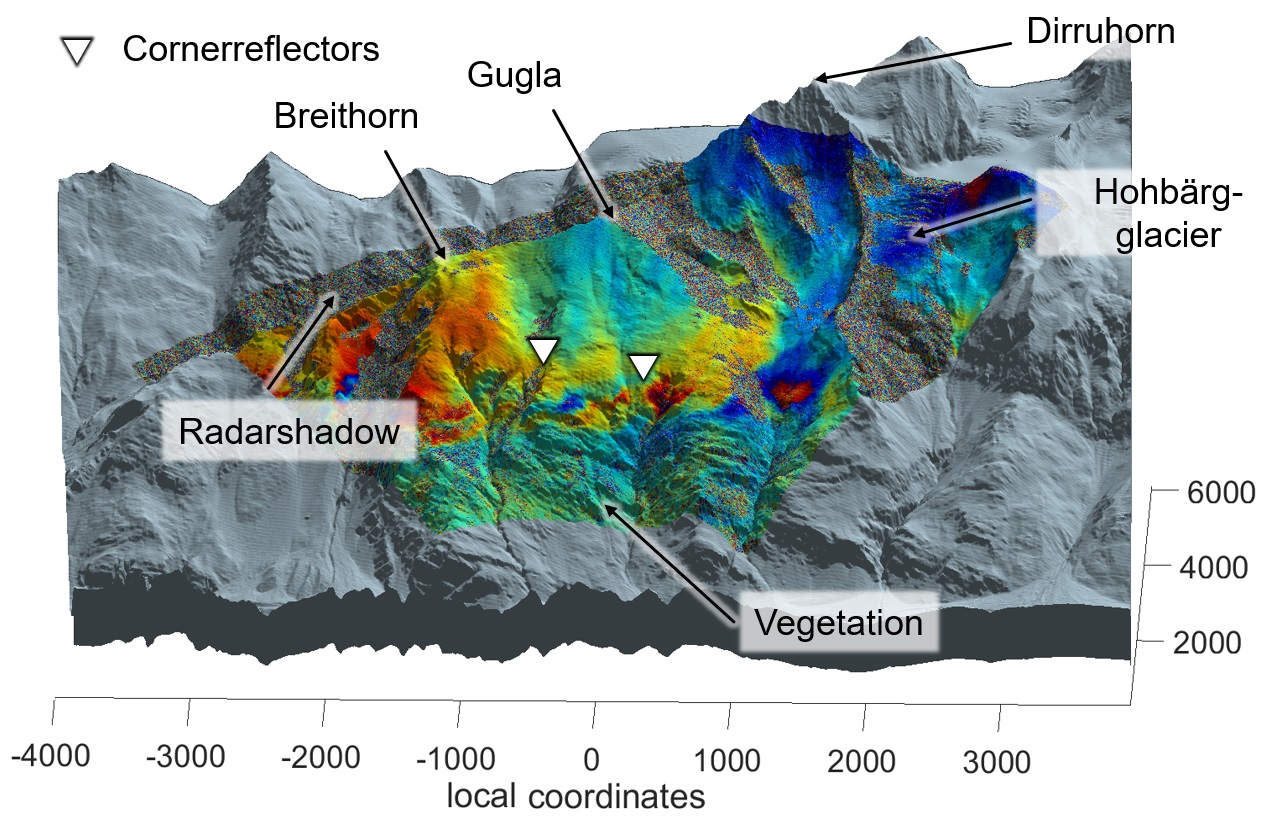
Image of a radar interferogram showing a wide variety of correlation structure — Fig 1: Radar interferometric data of a mountain range in southern Switzerland. Notice the wide variety of patterns visible at different regions in the image.

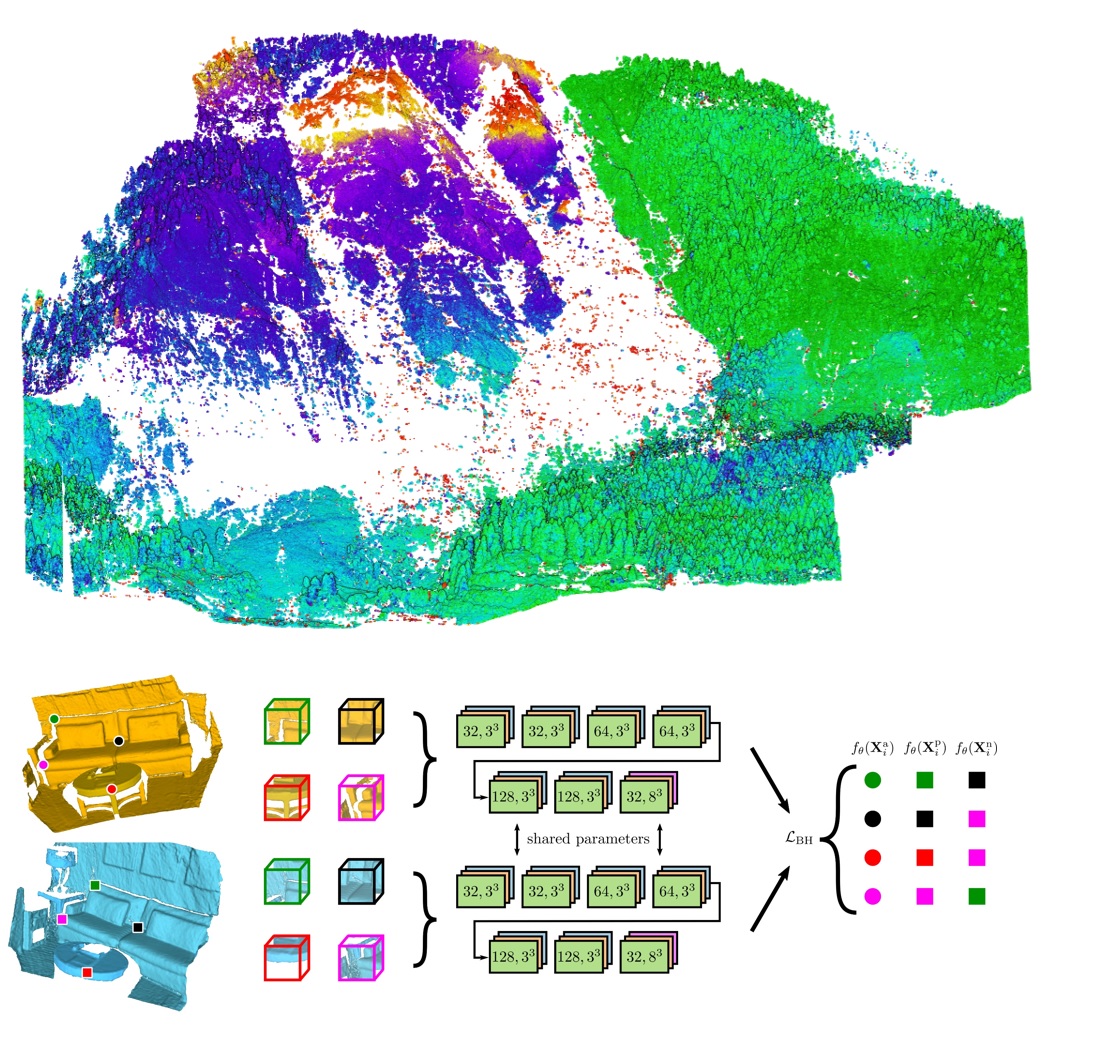
Extracting practically applicable knowledge from these type of data can be challenging; even more so when the results have to be reliable. Knowledge discovery and optimal estimation in a diverse collection of settings ranging from radar interferometric deformation analysis to point cloud processing and classical geodetic networks requires a unified approach. Choosing to be guided by stochastic optimality, we tackle real-world problems with methods from machine learning, functional analysis, explorative statistics and adjustment theory. This includes e.g. deep neural networks specifically trained to estimate deformation vector fields from pairs of 3D point clouds employing state-of-the-art loss functions and convolutional architectures.

Image of a deformation vector field produced by a neural network — Fig 2: Scheme and output of a neural network trained to map pairs of Point Clouds to deformation vector fields.

While in the most tractable cases, we rely on parameter estimation and hypothesis testing, nonlinear behavior is sometimes more easily handled by embedding it into an infinite-dimensional space that makes analyzing the relationship between features easy. Among other methods, reproducing kernel Hilbert spaces provide a framework for doing this systematically and make nonlinear quantities amenable to rigorous statistical methods thereby providing one more tool in the box used to get the most out of what our instruments provide.

Image of several mathematical quantities including trajectories, vector fields, manifolds. — Fig 2: Measurements can result in data of varying dimensionality and structure. Minimization in reproducing kernel Hilbert space yields estimators for underlying patterns in problems involving trajectories, vector fields and manifolds.